Quickstart: Nested Sampling with Ernest • ernest

library(ernest)
library(ggplot2)
library(posterior)
library(truncnorm)
library(LaplacesDemon)

Nested Sampling with Ernest

This vignette provides a hands-on introduction to nested sampling (NS) using the ernest package. You will learn how to:

Understand the role of model evidence in Bayesian inference and why it is difficult to compute.
Use prior transforms to define parameter spaces for NS.
Set up and run a nested sampling analysis in R with ernest.
Inspect, summarise, and visualise results from an NS run, including the evidence estimates and posterior samples.

Bayesian Model Evidence and Nested Sampling

In Bayesian inference, we use probabilities to represent our current beliefs about a model’s unobservable parameters (Ashton et al. 2022). When we gather new data, we update these beliefs using Bayes’ theorem: $P(\theta) = \frac{L(\theta)\pi(\theta)}{Z}$ where $\pi(\theta)$ is the prior distribution, $L(\theta)$ is the likelihood of a model given parameters $\theta$ and the data $D$ , and $P(\theta)$ is the posterior distribution of the parameters after our beliefs have been updated.

The denominator $Z$ is called the Bayesian evidence or marginal likelihood. In isolation, $Z$ serves to normalise $P(\theta)$ so that it is a well-conditioned probability distribution. If we reorganise Bayes’ theorem to isolate $Z$ , we see that calculating a model’s evidence involves integrating over all possible values of $\theta$ : $Z = \int_{\forall \theta} L(\theta) \pi(\theta) d\theta$ This allows us to use $Z$ as a parameter-independent measure of a model’s overall plausibility given some data. When comparing two models, the ratio of their respective evidences (called the Bayes factor) shows how much more the data support one model over the other, which forms the foundation of Bayesian model selection.

For most data and models, the evidence integral cannot be solved directly. Instead, researchers rely on estimation methods. Nested sampling (NS), introduced by Skilling (2004) and Skilling (2006), is designed to estimate $Z$ even when the posterior distribution is poorly conditioned (e.g., if $L(\theta)$ has multiple peaks or discontinuities along values of $\theta$ ). It accomplishes this by dividing the prior space $\pi(\theta)$ into many small nested shells or volumes. These shells are defined by the smallest likelihood value they contain, such that the volume of the cells containing the smallest value $L^*$ is given by $V(L^*) = \int_{L(\theta) > L^*} \pi(\theta) d\theta$ If we build many $V(L^*)$ across different values of $L^*$ , we can approximate the original multidimensional integral across the parameter space of $\theta$ with a one-dimensional integral over the sequence of $V(L^*)$ : $Z = \int_0^1 V^{-1}(L^*) dV$ where $V^{-1}(V(L^*)) = L^*$ exists. This requires us to estimate the volume of each shell $V$ , which we can do using the properties of the uniform order statistics (Speagle 2020).

NS generates this sequence of shells by generating a set number of live points within the prior space, then replacing the worst of these points with a new point from $\pi(\theta)$ with an additional likelihood constraint. This lets NS handle complicated likelihood surfaces, including those with multiple peaks or sharp transitions. In addition, NS naturally provides stopping rules, meaning the algorithm knows when it has gathered enough information to accurately estimate the evidence. As a bonus, the same samples used for evidence estimation can be repurposed to estimate the posterior distribution.

Nested Sampling with ernest

Here, we use an example from the documentation for the python NS package dynesty (Speagle 2020) to demonstrate how to use ernest to design, perform, and report nested sampling runs.

Defining Priors

Nested sampling operates by drawing samples from the prior, but for efficiency, ernest represents the prior space as points in a [0, 1)-unit hypercube. A prior transformation function must be specified to translate points from the hypercube into valid $\theta$ .

In ernest, you define priors using functions like create_uniform_prior() or by supplying a custom transformation to create_prior(). In addition to organising the prior into an object that ernest can use during NS, these functions also perform checks to help ensure your prior transformation function is size- and type-stable.

Example: Uniform Prior

In many cases, it is sufficient to define a prior with independently distributed uniform or normal distributions. Ernest provides convenience functions to build such priors with efficient prior transformation functions.

The following defines a uniform prior over $[-10, 10)$ for each parameter in 3D space:

prior <- create_uniform_prior(
  lower = -10,
  upper = 10,
  names = c("x", "y", "z")
)
prior
#> uniform prior distribution <uniform_prior/ernest_prior>
#> 
#> # A tibble: 3 × 3
#>   names lower upper
#>   <chr> <dbl> <dbl>
#> 1 x       -10    10
#> 2 y       -10    10
#> 3 z       -10    10

Example: Custom/Conditional Prior

For more complex priors, you must provide a custom function. In the case of prior spaces with independent marginals, this amounts to specifying a function that applies the inverse CDF for each component of $\theta$ .

Consider the following prior space with five dimensions: The first two are drawn from a bivariate Normal distribution, the third is drawn from a Beta distribution, the fourth from a Gamma distribution, and the fifth from a truncated normal distribution.

five_dim <- function(u) {
  x <- double(5)
  # MVN(mu = c(5, 2), Sigma = [5, 4; 4, 5])
  t <- qnorm(u[1:2])
  sigma_sqrt <- matrix(c(2, 1, 1, 2), nrow = 2, byrow = TRUE)
  mu <- c(5, 2)
  x[1:2] <- drop(t %*% sigma_sqrt) + c(5, 2)
  
  # Beta
  x[3] <- qbeta(u[3], shape1 = 2.31, shape2 = 0.627)
  
  # Gamma
  x[4] <- qgamma(u[4], shape = 5)
  
  # Truncated Normal
  x[5] <- qtruncnorm(u[5], a = 2, b = 10, mean = 5, sd = 2)
  
  return(x)
}
create_prior(
  fn = five_dim,
  names = c("MVN", "MVN", "Beta", "Gamma", "Norm[2, 10]")
)
#> New names:
#> • `MVN` -> `MVN...1`
#> • `MVN` -> `MVN...2`
#> custom prior distribution <ernest_prior>
#> 
#> # A tibble: 5 × 3
#>   names       lower upper
#>   <chr>       <dbl> <dbl>
#> 1 MVN...1      -Inf   Inf
#> 2 MVN...2      -Inf   Inf
#> 3 Beta         -Inf   Inf
#> 4 Gamma        -Inf   Inf
#> 5 Norm[2, 10]  -Inf   Inf

For more sophisticated priors (such as those for hierarchical models), you will need to build more involved prior transformation functions.

hierarchical <- function(u) {
  # mu ~ N(5, 1)
  mu <- qnorm(u[1], mean = 5, sd = 1)
  # log10(sd) ~ U[-1, 1]
  sd <- 10 ^ qunif(u[2], -1, 1)
  # x ~ N(mu, sd^2)
  x <- qnorm(u[3], mean = mu, sd = sd)
  c(mu, sd, x)
}
create_prior(
  fn = hierarchical,
  names = c("mu", "sigma", "x"),
  lower = c(-Inf, 0, -Inf)
)
#> custom prior distribution <ernest_prior>
#> 
#> # A tibble: 3 × 3
#>   names lower upper
#>   <chr> <dbl> <dbl>
#> 1 mu     -Inf   Inf
#> 2 sigma     0   Inf
#> 3 x      -Inf   Inf

Likelihood Function

Model log-likelihoods are represented in ernest with functions. These functions are expected to return a single scalar value for each possible $\theta$ within the prior space. If, for any reason, $\pi(\theta)$ contains regions where $\theta$ is invalid, ensure your likelihood function returns -Inf.

In this example, we use create_likelihood() to assign parameters to the LaplaceDemon density function for a multivariate normal distribution:

mu <- c(0, 0, 0)
C <- diag(1, 3)
C[C == 0] <- 0.95

loglike <- create_likelihood(
  \(x) dmvn(x, mu = mu, Sigma = C, log = TRUE)
)

Setting Up and Running the Sampler

Initialise the sampler with your likelihood and prior. The number of live points (n_points) controls the resolution of the sampling, with more points leading to more accurate estimates in exchange for longer run times.

sampler <- ernest_sampler(
  log_lik = loglike,
  prior = prior,
  n_points = 500
)
sampler
#> nested sampling specification <ernest_sampler>
#> • No. Points: 500
#> • LRPS Method: rwmh_cube
#> ernest LRPS method <rwmh_cube/ernest_lrps>
#> • Dimensions: 3
#> • No. Log-Lik Calls: 0
#> • No. Accepted Proposals: 0
#> • No. Steps: 25
#> • Target Acceptance: 0.5
#> • Step Size: 1.000

Run nested sampling for a fixed number of iterations or until the evidence estimate converges:

run <- generate(
  sampler, 
  max_iterations = 2000,
  show_progress = FALSE
)
#> ℹ Created 500 live points.
#> ✔ `max_iterations` reached (2000).
run
#> nested sampling results <ernest_run/ernest_sampler>
#> • No. Points: 500
#> • LRPS Method: rwmh_cube
#> ────────────────────────────────────────────────────────────────────────────────
#> • No. Iterations: 2000
#> • No. Calls: 35706
#> • Log. Evidence: -9.170 (± 1.762)

generate produces an ernest_run object that can be saved. You can continue a run by calling generate on a previously created ernest_run:

tmp_name <- tempfile("ernest_run.rds")
saveRDS(run, tmp_name)

continued_run <- readRDS(tmp_name)

run2 <- generate(continued_run, min_logz = 0.01, show_progress = FALSE)
#> ℹ Restored 500 live points from a previous run.
#> ✔ `min_logz` reached (0.00999454 < 0.01).
run2
#> nested sampling results <ernest_run/ernest_sampler>
#> • No. Points: 500
#> • LRPS Method: rwmh_cube
#> ────────────────────────────────────────────────────────────────────────────────
#> • No. Iterations: 6700
#> • No. Calls: 153206
#> • Log. Evidence: -9.078 (± 0.1249)

Inspecting and Summarising Results

The result object has a summary method for viewing evidence estimates, posterior samples, and diagnostics as a tidy tibble:

summary(run2)
#> nested sampling result summary <summary.ernest_run>
#> • No. Points: 500
#> • No. Iterations: 6700
#> ────────────────────────────────────────────────────────────────────────────────
#> • No. Calls: 153206
#> • Log. Volume: -20.19
#> • Log. Evidence: -9.078 (± 0.1249)
summary(run2)$run
#> # A tibble: 7,200 × 7
#>     call log_lik log_volume log_weight log_evidence log_evidence_err information
#>    <int>   <dbl>      <dbl>      <dbl>        <dbl>            <dbl>       <dbl>
#>  1     1  -2307.     -0.002     -2304.       -2313.                0           0
#>  2     2  -2239.     -0.004     -2236.       -2245.                0           0
#>  3     3  -2027.     -0.006     -2024.       -2033.                0           0
#>  4     4  -1998.     -0.008     -1995.       -2004.                0           0
#>  5     5  -1937.     -0.01      -1934.       -1943.                0           0
#>  6     6  -1886.     -0.012     -1883.       -1892.                0           0
#>  7     7  -1865.     -0.014     -1862.       -1871.                0           0
#>  8     8  -1831.     -0.016     -1828.       -1837.                0           0
#>  9     9  -1829.     -0.018     -1826.       -1835.                0           0
#> 10    10  -1803.     -0.02      -1800.       -1810.                0           0
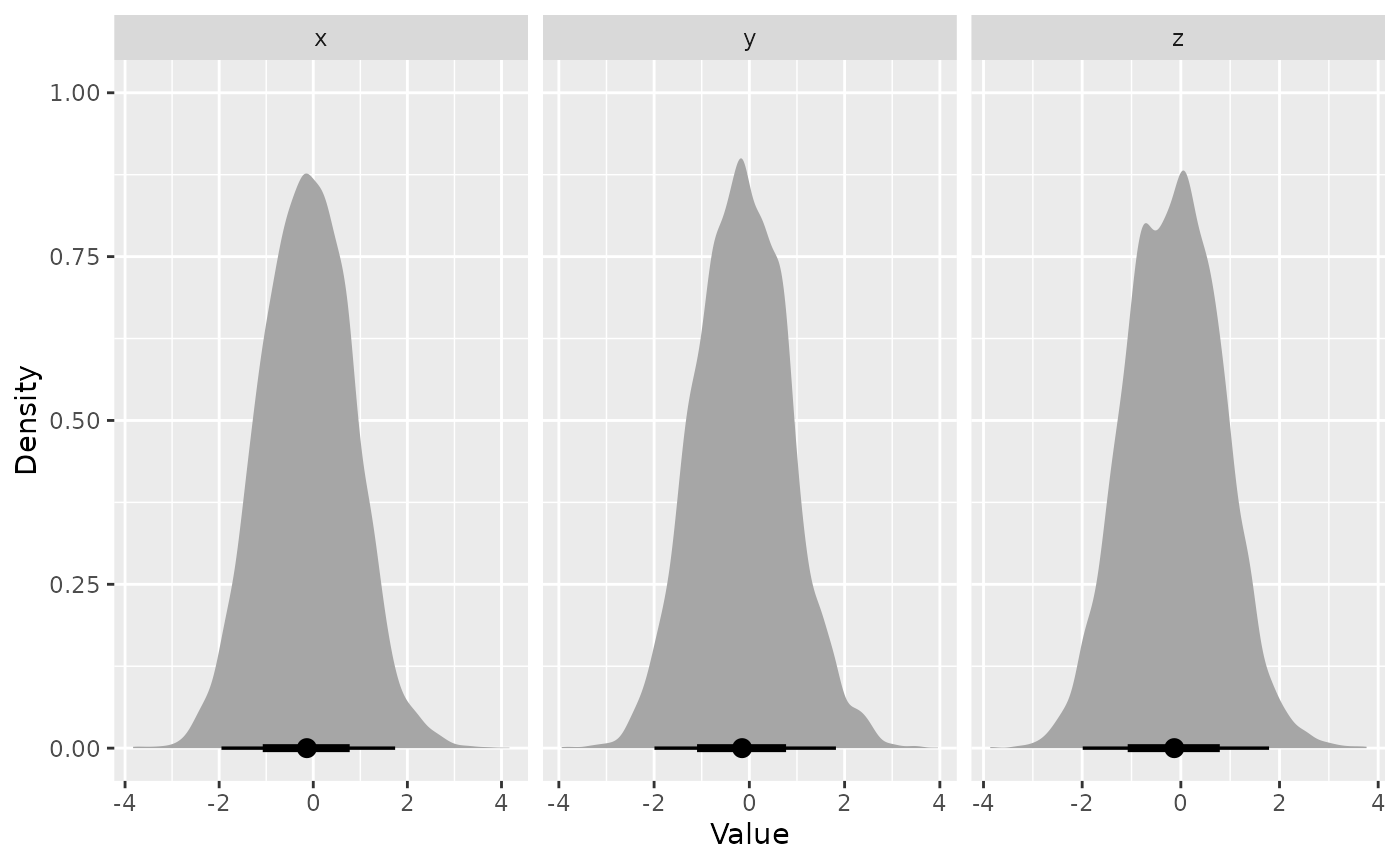
#> # ℹ 7,190 more rows

The posterior package offers methods for inspecting the points generated during a run:

library(posterior)
unweighted_post <- as_draws(run2)

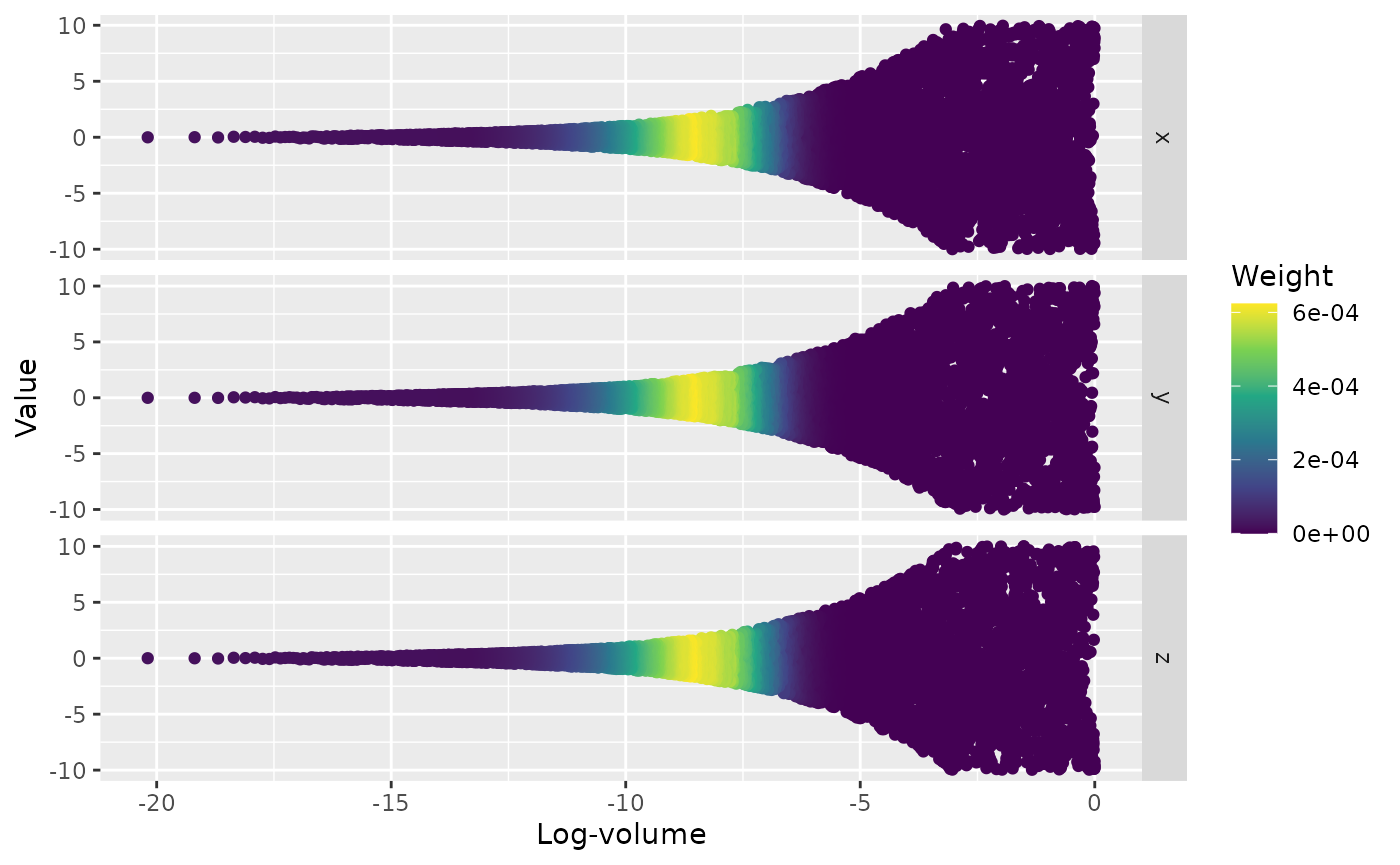
You can view the importance weight of each point and re-weight the sample to estimate the posterior distribution:

weights(unweighted_post) |> head()
#> [1] 0 0 0 0 0 0
weighted_post <- unweighted_post |>
  resample_draws()
posterior::summarise_draws(weighted_post)
#> # A tibble: 3 × 10
#>   variable    mean  median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>      <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 x        0.0179  0.00611 1.00  1.00  -1.62  1.69  1.20    1960.     13.6
#> 2 y        0.00645 0.00134 0.993 0.981 -1.63  1.66  1.18    1837.     13.3
#> 3 z        0.0159  0.00388 0.986 0.971 -1.61  1.62  1.17    1838.     14.7

Visualising Results

Ernest provides plotting utilities for evidence estimates and the posterior distribution.

Evidence evolution

plot(run2)

Posterior marginals

visualize(run2, type = "density")

Trace plots

visualize(run2, type = "trace", vars = c("x", "y", "z"))

Uncertainty and Resampling

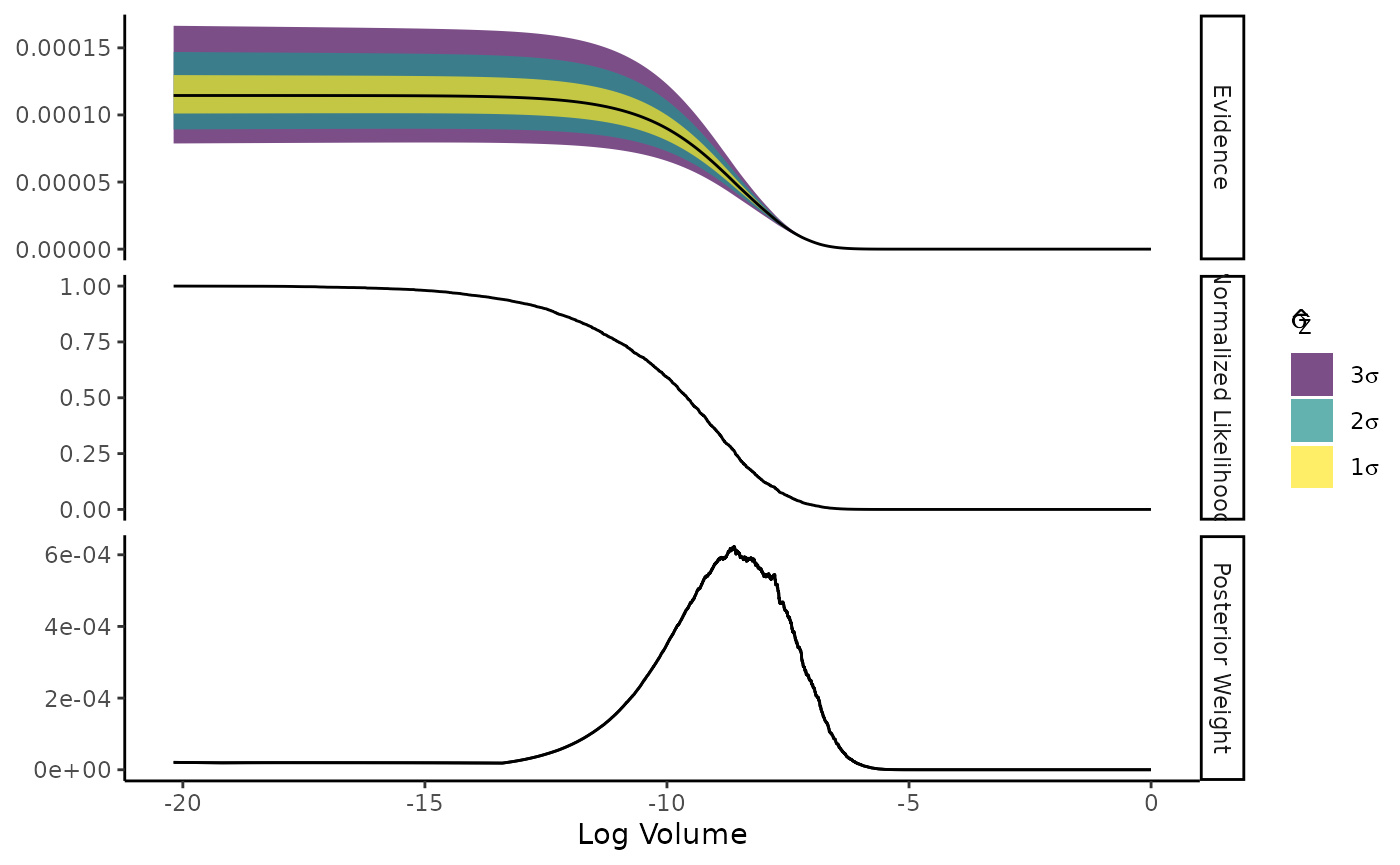
You can simulate the uncertainty of an NS run by generating random draws of the log-volume estimate at each iteration Higson et al. (2019). You can then visualise this uncertainty with the estimate’s plot method.

calc_sim <- calculate(run2, ndraws = 500)
calc_sim
#> evidence estimates <ernest_estimate>
#> 
#> No. of Simulated Draws: 500
#> Log. Volume: -20 ± 1.4
#> Log. Evidence: -9.1 ± 0.12
#> # A tibble: 7,200 × 4
#>        log_lik        log_volume    log_weight  log_evidence
#>     <rvar[1d]>        <rvar[1d]>    <rvar[1d]>    <rvar[1d]>
#>  1  -2307 ± NA  -0.0019 ± 0.0019  -2313 ± 0.82  -2313 ± 0.82
#>  2  -2239 ± NA  -0.0038 ± 0.0026  -2246 ± 0.82  -2246 ± 0.82
#>  3  -2027 ± NA  -0.0060 ± 0.0034  -2033 ± 0.86  -2033 ± 0.86
#>  4  -1998 ± NA  -0.0080 ± 0.0040  -2005 ± 0.75  -2005 ± 0.75
#>  5  -1937 ± NA  -0.0101 ± 0.0044  -1943 ± 0.81  -1943 ± 0.81
#>  6  -1886 ± NA  -0.0121 ± 0.0049  -1893 ± 0.85  -1893 ± 0.85
#>  7  -1865 ± NA  -0.0142 ± 0.0053  -1871 ± 0.82  -1871 ± 0.82
#>  8  -1831 ± NA  -0.0162 ± 0.0057  -1837 ± 0.80  -1837 ± 0.80
#>  9  -1829 ± NA  -0.0181 ± 0.0060  -1836 ± 0.75  -1836 ± 0.66
#> 10  -1803 ± NA  -0.0201 ± 0.0062  -1810 ± 0.76  -1810 ± 0.76
#> # ℹ 7,190 more rows
plot(calc_sim)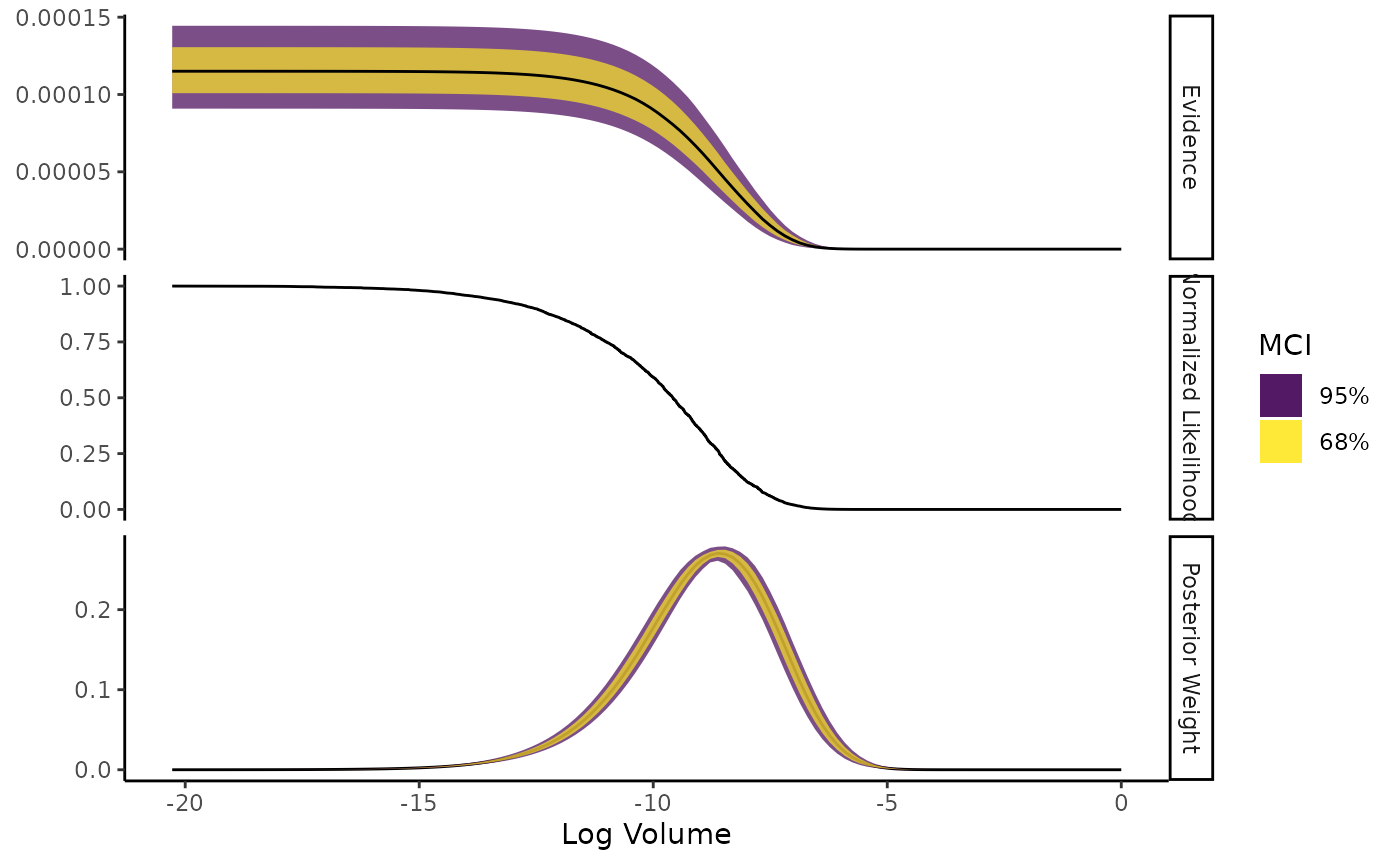

For more details on nested sampling, please refer to ernest’s documentation.

Ashton, Greg, Noam Bernstein, Johannes Buchner, Xi Chen, Gábor Csányi, Farhan Feroz, Andrew Fowlie, et al. 2022. “Nested Sampling for Physical Scientists.” Nature Reviews Methods Primers 2 (1). https://doi.org/10.1038/s43586-022-00121-x.

Higson, Edward, Will Handley, Michael Hobson, and Anthony Lasenby. 2019. “Nestcheck: Diagnostic Tests for Nested Sampling Calculations.” Monthly Notices of the Royal Astronomical Society 483 (2): 2044–56. https://doi.org/10.1093/mnras/sty3090.

Skilling, John. 2004. “Nested Sampling.” AIP Conference Proceedings 735 (1): 395–405. https://doi.org/10.1063/1.1835238.

———. 2006. “Nested Sampling for General Bayesian Computation.” Bayesian Analysis 1 (4): 833–59. https://doi.org/10.1214/06-BA127.

Speagle, Joshua S. 2020. “DYNESTY: A Dynamic Nested Sampling Package for Estimating Bayesian Posteriors and Evidences.” Monthly Notices of the Royal Astronomical Society 493 (April): 3132–58. https://doi.org/10.1093/mnras/staa278.